
Das aktuelle Rätsel |
| die aktuelle Aufgabe | bisherige Aufgaben | schwierige Aufgaben |
 |
|



| Dezember 2022 |
Let m and n be positive integers with gcd(m, n) = 1. Compute gcd(5m + 7m, 5n + 7n). |
| November 2022 |
If α, β and γ are the roots of x3 - x - 1 = 0, compute |
| Oktober 2022 |
Let ƒ be a random permutation on {1, 2, ..., 100} satisfying fƒ(1) > ƒ(4) and ƒ(9) > ƒ(10). The probability that ƒ(1) > ƒ(16) > ƒ(25) can be written as |
| September 2022 |
Auf den sechs Seiten eines Spielwürfels sind je einmal die negativen Augenzahlen -1, -3 und -5, sowie die positiven Augenzahlen +2, +3 und +6 aufgetrgen. Dieser Würfel wird dreimal geworfen.
|
| August 2022 |
Für welche k≥1 gibt es k aufeinanderfolgende natürliche Zahlen, deren Summe 100 ist? |
| Juli 2022 |
The numbers 1, 2, ..., 2012 are written on a blackoard. Each minute, a student goes up to the board, chooses two numbers x and y, erases them, and writes the number 2x + 2y on the board. This continues until only one number N remains. |
| Juni 2022 |
Auf einem rechteckigen Blatt Papier werden mit einem Lineal vier gerade Linien gezogen, die jeweils von Rand zu Rand verlaufen. Entlang dieser Linien wird das Blatt zerschnitten. a) wie viele Papierschnipsel können dabei entstehen? Geben Sie alle Möglichkeiten an. Begründen Sie, dass es nicht mehr als die genannten geben kann.Es werden nun n Linien auf dem Blatt gezogen. b) Finden Sie eine Formel, mit der die Maximalzahl der entstehenden Papierschnipsel berechnet werden kann. |
| Mai 2022 |
Aus Erfahrung weiss man, dass 10% der Passagiere eines Flugzeugs das vegetarische Menü wählen.
|
| April 2022 |
Wir betrachten Quader mit ganzzahligen Seitenlängen und denken sie uns aus Würfeln mit Seitenlänge 1 aufgebaut. So ein Würfel heisst innerer Würfel, wenn keine seiner Seiten von aussen sichtbar ist, ansonsten, also wenn wenigstens eine Seite von aussen sichtbar ist, heisst der Würfel äusserer Würfel.
Der abgebildete 3 x 4 x 7 Quader besteht aus 10 inneren und 74 äusseren Würfeln. |
| März 2022 |
Man ermittle alle reellen Zahlen x, die das folgende Ungleichungssystem erfüllen: |
| Februar 2022 |
Let d(n) denote the number of digits of n it its decimal representation. |
| Jänner 2022 |
Wir können N=100! auch schreiben als 30k*M, wobei M eine nicht durch 30 teilbare natürliche Zahl ist. |


Sommer 2022 |
Form a "triangle" with 10 blocks in its top row, 9 blocks in the next row, etc., until the bottom row has one block. Each row is centered below the row above it. Color the blocks in the top row red, white and vlue i$ Use these two rules to color the remaining rows of the triangle:
|
Frühling 2022 |
For any point E on the side BC of the square ABCD let E' be chosen on side CD so that DE' = CE, and let the lines AE and AE'
intersect the diagonal BD in points P and Q, respectively. If R is either point whose distance from P equals PB and from Q equals QD, then prove that ∠QRP = 60 °. |
Winter 2021 |
Find the value of the infinite product |
Herbst 2021 |
Let a, b, c, d be four real numbers such that Find the maximum possible value of |
Sommer 2021 |
A regular pentagon is constructed externally on each side of a regular pentagon of side 1. This figure is then folded and the two edges meeting at each vertex of the original pentagon but not belonging to the original pentagon are glued together. Determine the volume of water that can be poured into the resulting container without spillage. |
Früling 2021 |
Gesucht ist die Anzahl der geordneten Quadrupel (x1, x2, x3, x4) mit positiven, ungeraden Zahlen, sodass x1 + x2 + x3 + x4 = 98. |
Winter 2020 |
Wir gehen auf dem Kegelmantel von B nach A. 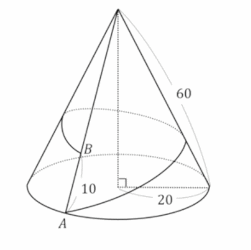
Berechne die Länge des Weges auf der Stecke BA der "bergab" geht. |
Herbst 2020 |
8 balls of radius 1 are placed in a cyclinder in two layers, with each layer containing 4 balls. Each ball is in contact with 2 balls in the same layer, 2 balls in the other layer, one base and the lateral surface of the cylinder. Then the height of the cylinder is ...... ? |
Sommer 2020 |
Gegeben ist das Produkt (1!) * (2!) * (3!) ... (97!) * (98!) * (99!) * (100!). Streiche einen der 100 Faktoren, sodass das verbleibende Produkt ein vollständiges Quadrat ist. |
Frühling 2020 |
Jede Seitenfläche eines regulären Dodekaeders liegt in einer eindeutig bestimmten Ebene. Diese Ebenen zerteilen den Raum in eine endliche Anzahl von disjunkten Raumteilen. Bestimme deren Anzahl. |
Winter 2019 |
50 Spielsteine stehen auf einem 10*10 Spielbrett sodaß,
Jeder Stein kann über seinen Nachbarn in das nächstliegende Feld springen. 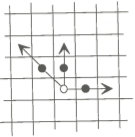
Ist es möglich die Spielsteine alle auf die linke Hälfte des Spielbretts zu bringen? |
Herbst 2019 |
Gegeben sei das gleichseitige Dreieck ABC mit der Seitenlänge a. Auf der Höhenlinie hc = CD befinden sich die Mittelpunkte der Kreise k1 und k2. Der Kreis k1 tangiert die Seite AB im Punkt D. Der Kreis k2 tangiert die Seiten AC und BC des Dreiecks. Die gemeinsamen Tangenten t1, t2 der Kreise laufen durch die Punkte A bzw. B. 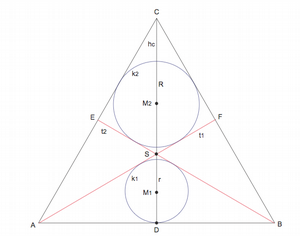
Berechne den Radius R von k2 wenn der Radius r für k1 gegeben ist. |
Sommer 2019 |
Let G = 1010100 (a.k.a. a googolplex). Then |
Frühling 2019 |
Determine all pairs of positive integers (a, b) such that |
Winter 2018 |
Nine balls, numbered 1, 2, ..., 9, are put randomly at 9 equally spaced points on a circle, each point with a ball. Let S be the
sum of the absolute values of the differences of the numbers of all two neighboring balls. Find the probability of S to be the
minimum value. |
Herbst 2018 |
A certain company wants to employ one secretary. Ten persons apply. What is the probability that the company hires the secretary with the best skills? |
Sommer 2018 |
Die Zahlen von 1,2,3, ... 100 sind in einer 10*10 Matrix derart eingetragen, dass aufsteigenden Zahlen, jeweils in benachbarten Zellen stehen (durch Seiten angrenzenden - nicht diagonal). Berechnen Sie die größtmögliche Summe der Zahlen die auf der NO-Diagonale stehen? |
Frühling 2018 |
Finden Sie alle positiv, ganzzahligen Tripel (a,m,n) mit a ≥ 2 und m ≥ 2, sodass an + 203 ein Vielfaches von am + 1 ist. |
Winter 2017 |
Eine gerade Pyramide mit quadratischer Grundfläche wird in eine Kugelmit Radius r eingeschrieben. 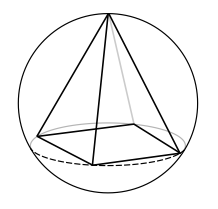
Berechnen Sie das maximale Volumen der Pyramide. |
Herbst 2017 |
Ein Mathematiker veranstaltet eine Sommerparty. Er hat einen dreieckigen Rasen vor dem Haus. Er treibt in jede Ecke seines Rasens und zusätzlich insgesamt n weitere Pflöcke am Rand oder im Inneren seiner Rasenfläche. Innerhalb werden genau k Pflöcke eingesetzt (0≤k ≤ n), und von diesen liegen keine drei auf einer gemeinsamen Geraden. Nun will unser Mathematik möglichst viele, nicht unbedingt gleich lange Hängematten an den Pflöcken befestigen, die einander natürlich nicht überschneiden dürfen. Auf diese Weise wird sein dreieckiger Garten in Teildreiecke zerlegt. Wieviele Teildreiecke sind maximal (in Abhängigkeit von k und n) möglich ? Richtige Lösungen eingesandt von:
|
Sommer 2017 |
Richtige Lösungen eingesandt von:
|
Frühling 2017 |
Gegeben ist ein Sack gefüllt mit 15 CUBES. Jeder CUBE ist würfelförmig und hat 6 Flächen auf denen positive ganze Zahlen geschrieben stehen. Bei jeder paarweisen Ziehung von 2 CUBES ist immer genau eine CUBE-Seite identisch. Berechne die kleinstmögliche Summe aller Zahlen auf allen Flächen aller CUBES. Richtige Lösungen eingesandt von:
|
Winter 2016 |
Gegeben ist folgende Figur: Der Radius des grossen Kreises ist 6 dm. Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Herbst 2016 |
Some unit cubes are assembled to form a larger cube. The some, but not all, of the faces of the large cube are painted. After the paint has dried, the large cube is disassembled and it is discovered that 218 of the unit cubes have some paint on them. What ist the size of the large cube? Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Sommer 2016 |
An algorithm is defined as follows: Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Frühling 2016 |
Betrachten wir die Zahlenfolge (bn) 1, 3, 4, 7, 11, 18, 29, .... Wie ergibt sich die nächste Zahl aus den vorhergehenden (rekursive Darstellung). Dann möchten wir aber z.B. die 57-te Zahl direkt berechnen, d.h. ohne alle 56 vorhergehenden Zahlen zu berechnen.
Weiter stellt sich die Frage: Gegen welche Zahl streben die Quotienten von aufeinanderfolgenden zwei Zahlen dieser Folge, d.h. welchen Grenzwert hat die Folge 3/1, 4/3, 7/4, 11/7, 18/11, 29/18, ..? Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Winter 2016 |
ABCD is a square and the semicircle on AB as diameter, center O1, lies within it. CG, where G lies on AD, touches this semicircle, and O2(r2) is the incircle of ΔCDG. An external common tangent of the semicircle and O2(r2) meets CD in R, BC in N, and intersects CG in M. The circle O3(r3) is the incircle of ΔCMN. Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Herbst 2015 |
A large marble of radius r is dropped into a conical drinking cup and comes to rest tangent to the cup. A larger marble of radius R > r is then dropped in and, as it turns out, is just touching the first marble as soon as it nestles into the cup (so the two spheres are tangent to each other, and each one is tangent to the cone in a circle of latitude). Find the volume of the region that lies between the two marbles and inside the cup.
|
Sommer 2015 |
Gesucht ist die Anzahl der geordneten Quadrupel (x1, x2, x3, x4) mit positiven, ungeraden Zahlen, sodass x1 + x2 + x3 + x4 = 98 Analytische Lösungen sind gefragt ! Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Frühling 2015 |
Die Zahlen 1,2,.......2n sollen derart in 2 Gruppen {a1,a2,a3,.... an} und {b1,b2,b3,.....bn} geteilt werden, sodaß gilt: a1 < a2 < a3 ...... < an-1 < an Berechne (auf analytische Weise) folgenden Ausdruck |a1 - b1| + |a2 - b2| + |a3 - b3| + .... + |an - bn| = ? Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Winter 2014 |
Gegeben sei ein m*n Netz aus Einheitsquadraten, entweder grün oder ungefärbt. Ein gefärbtes Quadrat ist ‚besonders’
Das gezeichnete 4*5 Netz hat keine ‚besonderen’ Quadrate !
Finde eine geschlossene Formel für die Menge aller 2*n Netze ohne ‚besondere’ Quadrate. Gesucht ist eine analytische Lösung! Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Herbst 2014 |
Sei X = {x1,x2,…,x9} eine Permutation der Menge {1,2,3,….9} und sei A die Menge aller X. f(X) = x1 + 2*x2 + 3*x3 + … 9*x9 Die Menge M = {f(X) / X ∈ A}. Bereche /M/ - d.h. die Anzahl der Elemente von M. Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Sommer 2014 |
Für ein gegebenes positves n, bezeichnet an die Anzahl einer n-stelligen ganzen Zahlen Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Frühling 2014 |
Gegeben sind die realen Zahlen a,b,c,d und e. Diese genügen den Bedingungen a + b + c + d + e = 8 Berechne den Maximalwert für e. Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Winter 2013 |
Zeige eine analytische Lösung von Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Herbst 2013 |
Berechne die Summe der unendlichen Reihe ln(2)/2 - ln(3)/3 + ln(4)/4 - ln(5)/5 + ... Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Sommer 2013 |
Wir schreiben die Zahlen mit den Ziffern 0 und 1 auf und ordnen sie der Größe nach. Wir streichen jene Zahlen mit zwei oder mehreren Einser nebeneinander. Wie lautet das 2013. Element der neuen Folge ? Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Frühling 2013 |
Gegeben ist die Folge an. Die ersten beiden Glieder sind Für jedes n>2 gilt
Beweise (analytisch!), dass die möglichen Folgen keine ganzzahligen Werte Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Winter 2012 |
Berechnen Sie die Wahrscheinlichkeit mit
Geben sie
Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Herbst 2012 |
Gegeben sei k eine positive ganz Zahl. Gesucht ist die Anzahl N(k) von Pukten (x,y,z) mit ganzzahligen Koordinaten die die folgenden Ungleichungen erfüllen: | x | ≤ k Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Sommer 2012 |
Mathematiker sind zu einem Bankett eingeladen. Sobald sich eine Person setzt, nimmt sie entweder das Glas Wein zu ihrer Linken oder zu ihrer Rechten, sind beide Gläser vorhanden, so wählt sie ein Glas nach dem Zufallsprinzip. Die Anzahl der Mathematiker an diesem Bankett ist groß. Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Frühling 2012 |
Alice hat viele Einheitswürfel (1*1*1) zur Verfügung; daraus baut Sie einen größeren Würfel und malt einige seiner Seiten (vollständig) an. Als Alice diesen großen Würfel wieder in seine Einheitswürfel teilt, stellt Sie fest, dass genau 60 Würfel völlig unbemalt sind. a) Was war die Seitenlänge des große Würfel und wie viele (und welche) Seiten hat Alice angemalt? Etwas später macht Alice dieses Spiel nochmals (mit weniger als 1000 Einheitswürfel). Als Sie mir die Anzahl der Einheitswürfel mit wenigstens einer bemalten Seite sagte, war es mir unmöglich die Würfelseite anzugeben. Hätte Sie mir jedoch gesagt, dass genau ein Würfel auf drei Seiten angemalt war, so hätte ich die Würfelseite angeben können. b) Was war die Seitenlänge des große Würfel und wie viele (und welche) Seiten hat Alice angemalt? Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Winter 2011 |
Bei der Produktion einer Uhr wurde leider ein Fehler gemacht: Stunden- und der Minutenzeiger sind identisch groß, und nicht unterscheidbar ! Unter der Annahme, dass die Bewegung beider Zeiger kontinuierlich ist, ist es Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Herbst 2011 |
Drei Kreise mit dem Radius 1cm sind entlang des Durchmessers AB eines Halbkreises mit dem Radius 2cm gezeichnet. Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Sommer 2011 |
Gesucht ist der geometrische Ort aller Punkte von dem jeweils zwei Tangenten zu den (klassischen) Kegelschnitten möglich sind, doch diese in P einen rechten Winkel bilden: a) Ellipse (x2/a2 + y2/b2 = 1) Eine möglichst geschlossene Darstellung ist gesucht. Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Frühling 2011 |
Ebene Geometrie: In einem Feld ist ein quadratisches Beet mit der Seitenlänge ‚x’ abgesteckt. Um dieses Beet ist ein Zaun errichtet – mit der Eigenschaft, dass von jedem Punkt des Zaunes, dieses Beet genau unter einem Winkel von 45° erscheint. Welche Gestalt hat der Zaun? Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Winter 2010 |
Gegeben sind 10 Punkte in gleichem Abstand auf einer Geraden. Darüber sind alle möglichen Halbkreise errichtet, deren Durchmesser jeweils 2 der 10 Punkte verbindet.
Wieviele Schnittpunkte haben diese Halbkreise? Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Herbst 2010 |
‚Schifferl’ versenken – ein wenig anders ! Wir spielen auf einem 2n*2n Brett und müssen jedes Feld einschwärzen und benutzen eine neue Technik. Diese ‚Farbspritztechnik’ ist leider noch sehr unzuverlässig ! Beim Versuch ein Feld zu färben (blaues Feld) schwärzen wir leider genau nur die vier umliegenden Felder, jedoch nicht das Feld was wir ursprünglich wollten; oder graphisch dargestellt:
Wieviele ‚Farbspritzer’ sind notwendig (in Abhängigkeit von n) um aller Felder zu schwärzen? Gesucht ist natürlich der minimalen Aufwand? Bitte geben Sie eine Lösungsvariante der Spritztechnik für ein 10*10 Brett an ! Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Sommer 2010 |
Gegeben ist ein hohler Würfel mit der Seitenlänge a. Eine Raumdiagonale ist ebenfalls eingezeichnet. Wie groß ist der Radius einer Kugel die alle drei Seitenflächen des Würfels und die Raumdiagonale berührt? Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Frühling 2010 |
Gegeben sind die Längen a und b mit a>b. a) In dieser Anordnung formen die beiden Strecken mit d ein Dreieck! Durch Rotation des Dreiecks um die Seite d entsteht ein Körper mit Volumen V(a,b,d) Wann ist V(a,b,d) ein Maximum ? b) In dieser Anordnung formen die beiden Strecken mit d ein Parallelogramm!
Wann ist W(a,b,d) ein Maximum ? Nachweis für Maximum ! Berechnen Sie die Maximalvolumina V(4,3,x) und W(4,3,y)! Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Winter 2009 |
Gegeben sind n rote und n blaue Punkte in der Ebene. Zeige, daß man jeweils eine (gerade) Strecke von jedem roten zu einem Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Herbst 2009 |
Gegeben sei ein Kreisausschnitt mit Radius R und Winkel α. Berechne den kleinsten Kreis mit Radius r = f(R, α) der diesen Kreisausschnitt völlig bedeckt?
Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Sommer 2009 |
Gegeben sind zwei einander berührende Kreise mit den Radien r und r+a. Die gemeinsame Tangente t schneidet die Koordinatenachsen in welchen Punkten ?
Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Frühling 2009 |
Wir alle kennen die Aufgabe mit der Wahrscheinlichkeit, daß zwei Personen in einer Gruppe den gleichen Geburtstag haben. Die heutige Aufgabe möchte wissen, wie groß die Gruppe sein muß, damit bei einer Wahrscheinlichkeit von =1/2 ich eine zweite Person finde, deren Geburtstag mit meinem (!) zusammenfällt ! Irgendein Zusammenhang zwischen beiden Aufgaben – wenn ja, welcher? Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Winter 2008 |
Ein auf allen Seiten mit Bilder beklebter (großer) Würfel ist aus 2*2*2 Einheits-Würfel zusammengestellt. Jede Position eines Einheitswürfels ist vorgegeben ! Gefragt ist die Anzahl der (zeitlich) unterschiedlichen Reihenfolgen in der man die Elementarwürfel zum großen Würfel zusammensetzen kann? Sind die Bezeichnung der Elementarwürfel unten 1,2,3,4 und oben 5,6,7,8 - welche Reihenfolgen sind dann möglich - und wieviel unterschiedliche gibt es? (z.B. 1,2,3,5, geht ---- aber 1,2,7,3 geht nicht - da der '3er'Würfel unten fehlt ? 1,5,2,6 geht ..... aber alle 5,x.... und 6,x..... sind ebenfalls unmöglich!) Zusatz: wie könnte die Lösung für einen 3*3*3 Würfel aussehen? Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Herbst 2008 |
Wir kennen alle das folgende Bild, sechs Kreise mit dem Radius r umgeben einen Kreis im Zentrum mit dem Radius r.
Wir modifizieren die Aufgabe etwas, wir fügen einen weiteren Kreis mit Radius r ein; Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Sommer 2008 |
Um 1985 entdeckten Chemiker die Fullerene, das ist Kohlenstoff der in festem Zustand auch in Form von käfigartigen Molekülen vorliegen kann. Das ‚Buckybaby’ C28 werden wir nun konstruieren: Gegeben ist der Tetraeder ABCD mit der Seitenlänge S. Wir zeichnen nun auf jeder Tetraederseitenfläche um seinen Schwerpunkt M ein regelmäßiges, kleines Sechseck mit der Seitenlänge ‚s’ derart, dass die Ecken auf den Seitenhöhen zu liegen kommen. Wir ergänzen diese Figur durch insgesamt 12 Fünfecke (wie eingezeichnet). Vier Punkte eines jeden Fünfecks sind ja gegeben. Der fünfte Punkt von drei Fünfecken liegt dann jeweils auf der Tetraederhöhe.
Wie groß muß die Seitenkante s' gewählt werden, damit auch die Kante XY die Länge s' hat? Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Frühling 2008 |
Gegeben ist folgende Figur. Berechnen Sie den Umfang des Rechteckes für beide Beispiele, wenn die Radien der Kreise sind: Beispiel a: r1= 1cm, r2= 2cm, r3= 3cm Beispiel b: r1= 2cm, r2= 3cm, r3= 4cm
Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Winter 2007 |
Sie füllen die Elemente einer m*n Matrix mit +1/-1 derart, daß das Produkt aller Elemente jeder Spalte und das Produkt aller Elemente jeder Zeile genau –1 ist. Wieviele unterschiedliche Matrizen mit dieser Eigenschaft gibt es ? Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Herbst 2007 |
Bilden Sie alle Polynome mit Koeffizienten aus der Menge (0,1,2,3) und f(2) = 2 Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Sommer 2007 |
Random-walk in drei Dimensionen. Ein Teilchen, startet im Ursprung eines 3-dimensionalen Raumes. Wir bilden um den Ursprung einen Würfel der Seitenlänge 2h derart, daß der Ursprung im Zentrum des Würfels liegt. Das Teilchen bewegt sich nun in einem Zickzackkurs rein zufällig mit der Schrittweite h und jeweils gleicher Wahrscheinlichkeit in Richtung einer der Seitenmitten der sechs Würfelflächen. Falls diese zufälligen Teilchenbewegungen sich beliebig lange fortsezten - wie groß ist die Wahrscheinlichkeit, daß das Teilchen im Laufe der Zeit wieder an den Ursprung zurückkehrt? Was passiert, wenn die zufällige Bewegung nicht in Richtung der Seitenmitten, sondern in Richtung der acht Würfelecken erfolgt? Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Frühling 2007 |
Wir haben einen Kartenstapel mit den Zahlen von 1 - 2007. Wir legen die oberste Karte dieses Stapels auf den Tisch, und die nächste wird dem Stapel ganz unten hinzugefügt. Die (neue) oberste Karte wird wieder auf den Tisch gelegt, rechts neben der ersten, und die nächste wieder unten hinzugefügt. Dies wird solange gemacht bis alle Karten auf dem Tisch liegen. Wir finden nun zu unserer Überraschung, dass die Karten auf dem Tisch in der Reihenfolge von 1-2007 liegen (von links nach rechts). Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Winter 2006 |
Gegeben sind 27 quaderförmige Steine mit den Abmessungen 2*1*0,5 (allgemein
a*b*c). Ist das möglich und wenn ja - geben Sie eine dieser Lagen explizit an. Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Herbst 2006 |
Aus mehreren kleinen, gleichgrossen Elementarwürfeln (1*1*1) können entweder zwei Quadrate oder ein grosser Würfel zusammengelegt werden. Die Kantenlänge des Würfels ist gleich der Differenz der Seitenlängen der Quadrate. Welches ist die minimale Anzahl an Elementarwürfel, die man dazu benötigt? Wie lautet die allgemeine Lösung? Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Sommer 2006 |
Gegeben ist ein Würfel mit der Seitenlänge 2r. Berechnen Sie den größtmöglichen Kugelradius dieser kleinen Kugeln, wenn
passen sollen. Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Frühling 2006 |
In einem Sekretariat treffen die zu schreibenden Briefe während des Tages ein, und werden immer auf (!) den Stapel der noch nicht erledigten Briefe gelegt. Wenn die Sekretärin Zeit hat, so nimmt Sie den obersten Brief und schreibt ihn. Insgesamt sind 9 Briefe zu schreiben und der Chef liefert Sie in der Reihenfolge 1,2,3,4,5,6,7,8,9 im Büro ab. Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Winter 2005 |
Es seien x1, x2, ... xn ... die Wurzeln des Polynoms Xn + Xn-1 + Xn-2 + ... + X + 1 Beweise, daß 1/(1-x1) + 1/(1-x2) + ... + 1/(1-xn) = n/2 Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Herbst 2005 |
Gegeben ist ein Würfel. Einer Seitenfläche ist der Kreis k1 eingeschrieben, einer benachbarten Seitenfläche ist der Kreis k2 umschrieben. Je ein Punkt bewegt sich auf k1 und k2. Was ist der geringstmögliche Abstand dieser beiden Punkte (d), und was sind die Koordinaten dieser Punkte. Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Sommer 2005 |
Gegeben ist ein Kreis mit dem Radius r. Ein Punkt auf dem Kreisumfang ist Mittelpunkt eines zweiten Kreises mit dem Radius x. Dieser zweite Kreis schneidet aus dem ersten Kreis eine Fläche A aus, die Restfläche des ersten Kreises bezeichnen wir mit B. Wie gross muss x gewählt werden, damit die Fläche A gleich der Fläche B ist. Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|
Frühling 2005 |
Die Eckpunkte eines Tetraeders mit der Kantenlänge r sind die Mittelpunkte von Kugeln mit dem Radius r. Bestimme das Volumen des entstehenden Schnittkörpers? Richtige Lösungen eingesandt von (in der Reihenfolge des Eintreffens):
|

Die rotierenden Körper wurden von Rüdiger Appel übernommen.
Im vorherigen finden sie einige schwierigere Aufgaben, welche vierteljährlich gestellt werden. Senden sie ihren Lösungsvorschlag ebenfalls per email an richard@mischak.com
Lösungen zu diesen Aufgaben können sie während einiger Monate einsenden, leider gibt es dafür noch keine Preise. Die Namen der Einsender korrekter Lösungen werden in der Reihenfolge des Eintreffens hier angeführt.
![]() Solltest du an
weiteren bisher gestellten Aufgaben interessiert sein, so
ersuchen ich um Kontakt.
Solltest du an
weiteren bisher gestellten Aufgaben interessiert sein, so
ersuchen ich um Kontakt.