Mit der Jagd auf Zahlen liegt ein in seiner Art einzigartige Projekt zuf Förderung der Mathematik vor. Ohne Zweifel erzeugt die nun auch praktisch erfrobte 'Jagd auf Zahlen und Figuren' vor allem Freude an der Mathematik. Das Lösen (interessanter) Aufgaben ist ja auch für die wissenschaftliche Mathematik zentral. Und insbesondere die hier zunächst fast spielerisch, dann zunehmend tiefer und 'ernsthafter' gestellten Aufgaben phaszinieren und bringen das Wesen der Mathematik in anregender Form nahe.

Die Jagd auf Zahlen und Figuren erinner mich an die Lotophagen aus der Odysse, die, wenn sie von einer Speise gekostet hatten nicht mehr aufhören konnten, von ihr zu essen.

tatsächlich scheint dieses in mehreren Jahren erarbeitete und erprobte Komzept hervorraged geeignet, Schülern und Jugendlichen durchaus verschiedenen Alters Mathematik als etwas Aufregendes, Interessantes und Schönes näherzubringen, in einer Form, die Ihnne gleiherart nützlich wie unterhaltsam und fordernd erscheint.

Und das genau ist ja das Weentliche, das in der Schule trotz allem Bemührens oft nicht entstehen kann, da die unterrichtlichen Rahmenbedingungen nicht umgangen werden können.

In diesem Sinn ist das Unternehmen auch keine 'Konkurrenz' zur Schule oder zur Tätigkeit der Lehrerinnen und Lehrer. Die Jagd auf Zahlen ist vielmehr Erweiterung und Ergänzung zum schulischen Alltag und kann - z.B. durch gemeinsamen Besuch - hervorragend genützt werden, den 'schulischen Alltag' zu erweitern und Heraus-forderungen einzubringen, die die Schule als solche naturgemäß nicht anbieten kann.

Die auch sehr gut durchdachte und gelungene Ausstellung steht auch aus international didaktischer Sicht sehr gut da, wenn eine derart saloppe Ausdruckweise gestattet ist. Derartiges entspricht zwar den international oft formulierten Ansprüchen, hat aber auch im Ausland kaum 'Konkurrenz'.

die Jagd auf Zahlen und Figuren kann man kaum durch Worte allein beschreiben, man muß (und sollte) sie erleben. Mathematik ist kein Zuschauersport; die eigene Tätigkeit, die Initiave und die Kreativität beim Lösen von Problemen ist das Wesentliche. Und genau diese Aspekte werden hier angesprochen. Viel Erfolg

Univ-Prof. Mag.Dr. Hans-Christian Reichel
Institut für Mathematik
Universität Wien

Dinge, die uns heute einfach und einleuchtend erscheinen, wie etwa die Art, die Zahlen zu schreiben, mit Ihrem 'Stellenwertsystem' und der Einführung eines Symbols für Null, das dem Ganzen erst die Vollendung gab, erforderten zu ihrer

Erfindung unglaubliche Mühe.

Selbst noch einfachere Dinge, die den Kern des mathematischen Denkens bilden, die Abstraktheit und Allgemeingültigkeit der Zahl, mußten erst in jahrelangen Bemühungen errungen werden; Ihre Schöpfer sind jedoch dahingegangen, ohne eine Spur zu hinterlassen.

Auf dem Weg der Mathematik von der Vergangenheit in die Gegenwart stoßen wir von Anfang an auf zwei grundleged Tendenzen, die die Entwicklung der Mathematik beherrschen. Wir können sie etwa die diskrete und die kontinuierliche Betrachtungsweise nennen.

Die diskrete Betrachtungsweise

ist bestrebt die ganze Natur und die ganze Mathematik mit Hilfe von einzelnen individuell erkennbaren Elementen (sozusagen atomistisch) zu beschreiben - wie etwa durch die Zahlen 1,2,3 ...

ist Domäne der Algebra, der Zahlentheorie und der symbolischen Logik.

Die kontinuierliche Betrachtungsweise

versucht alle Naturerscheinungen - der Flug eines Vogels, die Bahn eines Balls in der Luft, der Fall eines Regentropfens - und eine Unzahl mehr durch Heraklits mystische Formel 'Alles fließt' zu erklären. Was mit 'kontinuierlicher Bewegung' gemeint ist, glauben wir intuitiv zu wissen. Die Bewegung ist gleichmäßig, nicht ruckweise und ohne Pausen, oder allgemeiner gesagt, für den Begriff der Kontinuität sind die individualistisch auftretenden Zahlen 1,2,3.... nicht das geeignete mathematische Bild.

Dieses System das mit den Buchstaben I,V,X,L,C,D,M arbeitet ist bei großen Zahlen schlecht anwendbar. Leider sind auch die einfachsten Operationen damit sehr aufwendig.

Versuchen Sie eine einfache Multiplikation nachzuvollziehen

LVII mit XXXVIII = MMCLXVI !

Zwischen zwei Punkten auf einer Strecke können wir ganz gleich wie eng sie beieinander liegen mögen, immer einen weiteren Punkt finden. Es gibt keinen 'nächsten' Punkt, keinen kürzesten Schritt von einem Punkt zum nächsten Punkt - es gibt überhaupt keinen nächsten Punkt.

Diese Auffassung führt uns mit Newton und Leibniz in die Infinitesimalrechnung und ihre zahllosen Anwendungen in Technik und Naturwissenschaften.

Pythagoras pflegte zu sagen "Die Zahl regiert das Universum",

Galilei pflegte zu sagen "Das große Buch der Natur ist mit mathematischen Zeichen geschrieben" doch bald werden wir erkennen, daß wir dieses besondere Schriftsystem verwenden, weil wir es zu unserem eigenen besseren Verständnis erfanden.

Vielleicht erfinden wir eines Tages noch eine ausdruckfähigere Kurzschrift als die Mathematik, um unsere Erfahrungen vom physikalischen Universum miteinander in Beziehung zu setzen.

Die Mathematik hatte also vier große Zeitalter

• das Babylonische

• das Griechische

• das Newtonsche

• das moderne, ab 1800 bis heute

 Eine der wichtigsten Aufgaben der heutigen Mathematik ist, das Diskrete mit dem Kontinuierlichen in Einklang zu bringen, beide Auffassungen zusammenzufassen und Unklarheiten zu beseitigen.

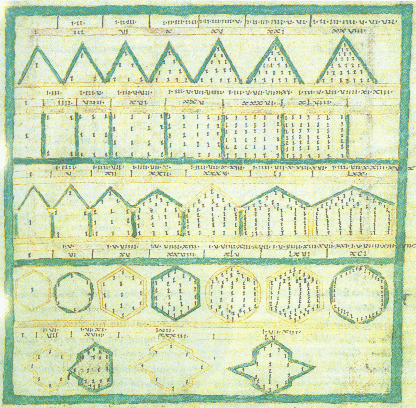
Dreiecks-, Vierecks- und Fünfeckszahlen aus pythagoräischer Zeit
Quelle: De Arithmectica, BNF, paris

Zahlzeichen und -systeme

In der Anfangszeit der mathematischen Betätigung drückte man Rechnungen, Lehrsätze und Formeln nur in Worten aus. Wegen der Umständlichkeit und Unübersichtlichkeit des Verfahrens wurden für häufig vorkommende Ausdrücke Abkürzungen üblich. Schon die Griechen bezeichneten. Punkte, Linien und Flächen mit Buchstaben.

Zahlenmythen mischen sich mit Historie und der Aberglaube beeinflußt Zeitgeschichte, und zwar nachhaltiger als man gemeinhin annimmt.

• In Asien findet man keinen Parkplatz und keinen Flugzeugsitz mit der Nummer vier, denn das Wort 'shi' das die Zahl Vier benennt steht auch für Tod.

• In Italien bringt Freitag der 17. Unglück, so entschloß sich einst Napoleon seinen Staatsstreich vom 17. auf den 18. Brumaire der Jahres 1799 zu verschieben.
  Es wurde niemals ein Renault 17 verkauft - er wurde zu 117 umgetauft!

• In Amerika wird das 13.Stockwerk oft ausgelassen, da 13 Unglück bedeutet. Es fallen sogar Flugzeugingenieure auf Zahlenmagie herein, wie ließe sich sonst die Bezeichnungen der Boing Typen 707, 727, 737, 757, 767, 777 erklären.

Die irrationale Angst vor Zahlen hat auch jahrhundertelang den Durchbruch der heute als 'arabisch' bekannten Ziffern verhindert. Der Zahlenaberglaube war im Bewußtsein der Kirche des Mittelalters so tief verwurzelt, daß man den gemeinen Menschen das Rechnen mit arabischen Zahlen vorenthielt.

Erst mit der Französischen Revolution im Jahre 1789 setzten sich die arabischen Ziffern endgültig gegenüber den römischen Ziffern durch.

Mit kleinen Steinen (lateinisch: calculi) oder mit Holzstäbchen zählten schon die Steinzeitmenschen. Mayas, Griechen, Babylonier und Ägypter, sie alle schlugen ähnliche Wege ein - sie erkannten, daß ein gezeichnetes Symbol, beispielsweise ein Vogel in ägyptischer Hieroglyphen oder eine Blume bei den Mayas, am besten geeignet ist,

eine bestimmte Zahl darzustellen, so entstanden die Ziffern. Die ersten Zahlzeichen finden wir schon vor den ersten Schrifterfindungen in Mesopotamien und Ägypten. Gezählt wurde hauptsächlich gleiche Gegenstände und gleiche Zeitabschnitte. Wenig später wurde in einem ähnlichen Verfahren das Alphabet entwickelt. Obwohl ein Zeichen für eine Zahl etwas ganz anders ist, als ein alphabetisches Zeichen.

Bald stellte sich das Problem mit wenigen Zeichen alle Zahlen darzustellen. Es ist wahrscheinlich, aber nicht sicher, daß die Wahl der 10 als Grundzahl mit den 10 Fingern zusammenhängt. In alten Zahlmaßen, Dutzend, Groß finden sich Hinweise auf ein verschwundenes 12-system; das französische quatre-vingt (für 80) deutet auf ein (nicht-positionelles) 20-system. Unser Zeitmaße (60', 60 sek) und die Winkeleinteilung in 360° erinnern an das 60-system der Babylonier.

Die zweite entscheidende Etappe auf dem Weg zur Entwicklung einer numerischen Ordnung besteht darin, durch die jeweilige Position der Ziffer ein Zahlensystem zu erstellen. Schon 1900 v.Chr. benutzten die Babylonier diese Methode. Die Chinesen entdeckten sie erst zu Beginn unser Zeitrechnung, die Mayas zwischen dem vierten und sechsten Jahrhundert, die Altägypter nie. Wenig später wurde in einem ähnlichen Verfahren das Alphabet entwickelt. Obwohl ein Zeichen für eine Zahl etwas ganz anders ist, als ein alphabetisches Zeichen.

Zur Ausbildung eines Positionssystems fehlte aber vor allem die konsequente Benutzung eines Zeichens für 'leere Stellen' die Null also. Die epochale Entdeckung - die der Null - mußte bis zum 4.Jahrhundert n.Chr. warten. Das Denken eines Anfangs und eines Endes ging einher mit der Erfindung der Null; die (indische) Erfindung der Null bedeutete ursprünglich paradoxerweise ein Symbol für das 'Nichts'. Das Symbol Null deutet auf etwas, das nicht ist, aber war oder möglicherweise sein wird. Mit der Einführung der Null hat sich der Zahlbegriff hinreichend von den konkreten Gegenständen gelöst.

Trotz aller Technologie wird auch im Klassenzimmer der Zukunft der Lehrer nicht fehlen. Die sozialen Kontakte und das Erleben der Schülergemeinschaft kann der Computer nicht ersetzen. Die neuen technischen Möglichkeiten sollen genutzt werden, um sich schneller und bequemer Informationen zu besorgen - sie sind aber kein Ersatz für zwischenmenschliche Beziehungen in der Klasse.

Wir wissen aus unserer Kultur- und Mediengeschichte, daß neue Technologien und Erfindungen immer wieder Erlösungssehnsüchte und Untergangsphobien auslösten. Alles was fehlerhaft oder unmöglich war, soll mit den neuen Technologien überwunden werden. Auch die Pädagogik erhofft sich immer wieder Wunder von den neuen Möglichkeiten.

Die heutige Technik (Computer, Netzwerk und Multimedia) kann Lernen erleichtern, aber sie löst nicht die Probleme des Schulunterrrichts. Internet, lokale Netzwerke, CD-ROMs und vieles mehr kann sinnvoll verwendet werden. Hier sollen kurz einige Schulen und Projekte vorgestellt werden, die damit Erfolg hatten.