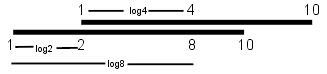World Mathematical Year 2000

• the determination of great mathematical challenges of the 21st century,
• the promulgation of mathematics, both pure and applied, as one of the main keys for development, and
• the recognition of the systematic presence of mathematics in the information society (=the image of mathematics).

Mathematische Spiele - spielerische Mathematik

Wo kann man Spiele sehen, die Wissenswertes über die Mathematik vermitteln und einfach zu verstehen sind? Bleiben nur Trivialspiele, bei denen man höchstens Wissensunwertes dazulernt, oder gibt es ein nachdrückiches Nein - zum Beispiel die Jagd auf Zahlen und Figuren!

Noch im 17.Jahrhundert erzeugten 'negative' Zahlen entschiedenen Widerstand bei den meisten Mathematikern. Descarte etwa prangerte negative Wurzeln als 'falsche Wurzel' an und auch Blaise Pascal war noch der Überzeugung, es könne keine Zahl keiner als Null geben! Leibniz, der zwar zugab, daß negative Zahlen zu absurden Schlußfolgerungen führen könnten, verteidigte sie als ein nützliches Hilfsmittel für die Durchführung von Rechnungen.

Auch in der Mathematik ist es nicht möglich zu entscheiden, welche Periode die wahrhaft 'größte' Epoche genannt werden soll, da jede neue Generation auf dem Werk ihrer Vorfahren aufbaut. Die Gegenwart ist von einem beispiellosen Maß an mathematischen Forschungstätigkeit geprägt. Ich möchte nur die wichtigsten kurz aufzählen:

Daß Oberflächen, wie zum Beispiel der Fußboden, nicht nur mit drei-, vier- und sechseckigen Brettern regelmäßig belegt werden können, zeigen schon die berühmten Graphiken vom M.C.Escher. Der Physiker Roger Penrose entwickelte daraufhin die theoretischen Grundlagen, die das 'Parkettieren der Ebene' zu einem Zweig der mathematischen Wissenschaft machten. Mit 'Fractiles' kan man diese Theorie ohne viel Wissenschaft ohne viel Theorie selber ausprobieren.. Diese Elemente lassen sich zu sehr phantasiereichen Mustern zusammensetzen und ergeben die nötigen Ideen zur kommenden Renovierung der Küche oder des Badezimmers! Das gleiche gilt auch für den dreidimensionalen Raum!

Geheimcodes sind ein anderes sehr aktuelles Kapitel der Mathematik. Heute dreht sich alles um die 'rasche' Faktorisierung großer Zahlen und die rechnerische Schwierigkeiten, die sich dabei ergeben können. Eine der sichersten Formen der Verschlüsselung von Nachrichten macht sich nämlich gerade die Schwierigkeit zunutze, sehr große Zahlen in faktoren zu erlegen. Die Geschichte, wie sich ein scheinbar nutzoser und esoterischer Bereich der reinen Mathematik zur Grundlage unserer heutigen, modernen Sicherehitssysteme mauserte, ist eine der interessantesten mathematischen Entwicklungen unseres Jahrhunderts. Geheime Codes zu verwenden ist nicht neu. Schon Julius Cäsar verschüsselte während des Gallischen Krieges die Botschaften an seine Generäle. Heute gibt es wirtschaftliche und politische Gründe um Nachrichten so zu schützen, daß sie nicht in falsche Hände gelangen.

In einem typischen 'Verschlüsselungssystem' vereinbaren Absender und Empfänger im voraus einen gehiemen Schlüssel, den sie dann zur Übermittlung ihrer Nachrichten benutzen. Solang der Schlüssel geheim gehalten wird, sollte das System - vorausgesetzt es ist gut - sicher sein. Ein Beispiel dafür ist das amerikanische System 'Data Encryption Standard (DES)', dessen Schlüssel eine Zahl sein muß, die in der binären Schreibweise 56 Bits benötigt. Warum muß der Schlüssel so eine große Zahl sein? Nun, niemand macht ein Geheimnis daraus wie das DES-Verfahren funktioniert. Alle Einzelheiten lassen sich in der Fachliteratur nachlesen. Theoretisch könnte der Feind also unseren Code knacken, indem er nacheinander alle Schlüssel ausprobiert - doch dies ist eine so enorme Anzahl, daß es eine praktische undürchführbare Aufgabe ist. Obwohl diese DES-Systeme heute weit verbreitete sind, haben sie doch einen offensichtlichen Nachteil. Bevor sie benutzt werden können, müssen sich die Parntner über den Schlüssel verständigen. Da der Schlüssel sicher nicht über das öffentliche Kommunikationsnetz mitgeteilt werden soll, müssen sich die Partner treffen, oder zumindest über einen vertrausenswürdigen Kurier verfügen, der die Schlüssel übermittelt. Das System eigent sich nicht für die Kommunikation zwischen Partnern, die sich nicht persönlich kennen. Insebsondere eignet es sich nicht für den Einsatz im internationalen Bank- oder Wirtschaftswesen, da es in diesem Bereich oft notwendig ist, vertrauliche Nachrichtn an unbekannte Personen im fremden Ländern zu schicken. Abhilfe dazu schafft ein völlig neuartiges System der Kodierung - public key encryptography - im Jahre 1975 erstmals vorgestellt. Hier wird nicht nur ein Schlüssel verwendet sondern zwei - einer zu Kodieren, der öffentlich bekannt ist, und ein anderer zum Dekodieren, der geheim ist. Das Verfahren, das von Ronald Rivest, Adi Shamir und Leonard Adleman vom MIT entwickelt wurde ist heute als RSA-Verfahren bekannt. Die Sicherheit beruht also gerade auf der ineffizienz der heutigen Methoden der Faktorisierung sehr großer Zahlen. Heute werden oft 100-stellige Primzahlen zur Erzeugung eines 200-stelligen öffentlichen Schlüssels verwendet.

Wie lange ist die Küste Großbritanniens ?

Diese Frage war der Gegenstand eines epochemachenden Artikels, der 1967 unter gleichem Titel in der Zeitschrift Science erschien. Der Verfasser war Benoit Mandelbrot, ein brillianter fanzösischer Mathematiker, der für IBM in New York arbeitete. Auf dem ersten Blick scheint auch diese Frage durchaus harmlos zu sein. War würde erwarten, daß sich eine einigermaßen genaue Antwort mit Hilfe einer Straßenkarte oder durch Anfertigung von Lutaufnahmen ermitteln läßt. Doch weit gefehlt ! - Es gibt keine richtige Antwort !!! Diese aufsehenerrende Schlußfolgerung hatte Mandelbrot aufgrund folgender Argumentation: Angenommen wir vermessen die Küste mit einem Flugzeug aus ca 10 000m Höhe. Aus dieser Höhe läßt sich eine Vielzahl kleiner Buchten und Vorsprünge nicht erkennen. Wir machen die gleiche Messung aus einem kleinen Flugzeug aus 500m Höhe - und es werden viele zusätzliche Detais sichtbar. Stellen wir uns nun vor, wir machen uns zu Fuß auf den Weg um die Küste mit einer Genauigkeit von 1m abzumessen. Unregelmäßigkeiten, die aus der Luft nicht sichtbar sind, führen uns zu einem noch weitaus besseren Ergebnis als die beiden ersten Messungen. Doch nun wiederholen wir die Messung mit einer Genauigkeit von 1cm ...... Schnell ist man beim Maßstab eines Kieselsteines, eines Sandkornes, eines Moleküls, und das Meßergebnis wächst ins Unendliche !!!

Doch was hat diese Küstenlinie nun mit der Mathematik zu tun? Da sie im wahrsten Sinn des Wortes eine Kurve darstellt, könnte man meinen sie ist eindimensional. Dies stimmt jedoch nicht. Obwohl jede einzelne nach obigem System konstruierte Approximation der Küstenlinie eindimensional ist, gilt dies für die Grenzkuve nicht. Anläßlich der unendlich vielen wechselnden Richtungen der Kurve ist es auch nicht länger gerechtfertigt von 'Richtung' zu sprechen - wir haben damit die Welt unserer bekannten Mathematik verlassen. Der 'Dimensionsbegriff' muß angepaßt werden und durch ein Merkmal der Selbstähnlichkeit definiert werden. Für die Küstenlinie erhalten wir etwa D=1,2618. Gebilde die eine gebrochene Dimension aufweisen wurden 1977 von Mandelbrot als Fraktale bezeichnet und die Wissenschaft, die sich damit befaßt wird als fraktale Geometrie bezeichnet.

Knoten sind für den durchschnittlichen Pfadfinder sehr bald kein Problem - doch auch hier hat sich ein völlig neuer Zweig der Mathematik erst 1984 ergeben. Die Knotentheorie ist ein Unterbereich der Topologie. Es werden im dreidimensionalen Raum 'Knoten' mathematisch betrachten. Ein Knoten ist nicht anderes als eine geschlossene Schlinge, die mittels einer Schnur, eines Seils oder eines beliebigen anderen Materials gebildet wird. Wie entscheide ich also ob zwei Knoten wirklich verschieden sind? Wie entscheide ich überhaupt ob das Kabel des Rasenmähers nur verheddert ist - oder wirklich verknotet? Zauberkünstler machen von diesen beeindruckenden 'scheinbaren Knoten' ausgiebig Gebrauch. Am Anfang unseres Jahrhunderts wurden die Primknoten untersucht und sie wurden nach ihrer Kreuzungszahl klassifiziert. Da diese Kreuzungszahl eine Knoteninvariante ist, kann sie zur Untersuchung nichtäquivalenter Knoten herangezogen werden - doch leider können Knoten die nicht äquivalent sind die gleiche Kreuzungszahl haben. 1960 erzielte John Horton Conway eine neue und effektive Notation für Knoten. Doch bald stellt sich auch heraus, da jedem Knoten eine (unendliche) Knotengruppe zugeordnet werden kann. Angesichts der schweren mathematischen Geschütze die notwendig geworden sind, fragt sich der Leser, ob es denn nicht eine einfache Methode gibt Knoten zu unterscheiden. Die 1928 von J.W. Alexander gefunden wurden- Alexander-Knoten-Polynome - waren ein ersten Schritt, jene von 1984 erweiterte Knoten-Polynom-Darstellung half weiter, doch noch immer ist es nicht möglich mit Polynomen zwischen allen nicht äquivalenten Knoten zu unterscheiden.

Kurz möchte ich noch die Katastrophentheorie (=angewandet Theorie der Mannifaltigkeiten) erwähen. Die meisten Topologen würden diese Theorie der Mannigfaltigkeiten als die zentrale Triebkraft ihrer Disziplin betrachten. Obwohl die Topologie ein überaus leicht zu beschreiben ist, ist es ein schwieriges Teilgebiet der Mathematik. Intuitiv kann man sich die topologische Abbildung als eine stetige Deformation vorstellen, bei der das Objekt gebogen, gedehnt, zusammendegrückt oder verdreht wird oder aber eine Kombination solcher Verformungen. Man geht davon aus, daß das deformierte Objekt vollständig elastisch ist und beliebig viele solcher Verformungen unbschadet überstehen. Die obige Beschreibung mit Dehnen, Biegen und Drücken muß unvollständig sein, da die Topologie sich auch mit drei-, vier- und fünfdimensionalen Objekten beschäftigt. Viel Verwirrung verursacht auch hier der Begriff der Dimension. Die Oberfläche einer Kugel ist eine zweidimensionale Fläche - sie läßt sich allerdings nur in einem dreidimensionalen Raum darstellen.

Doch was wurde noch Anfang dieses Jahrhunderts über die Mathematik gesagt? G.H. Hardy schrieb 1940

... die Stukturen des Mathematikers müssen wie jene des Malers oder des Dichters schön sein; die Gedanken müssen sich wie die Farben oder die Worte harmonisch zusammenfügen. Schönheit ist der erste Prüfstein; eine häßliche Mathematik kann in der Welt nicht bestehen. Es mag sehr schwierig sein, mathematische Schönheit zu definieren, doch trifft dies für Schönheit jeder Art zu - wir wissen vielleicht nicht genau was wir unter einem schönen Gedicht verstehen, doch hindert uns dies nicht, es als solches zu erkennen, wenn wir es lesen.

Dr. Richard Mischak